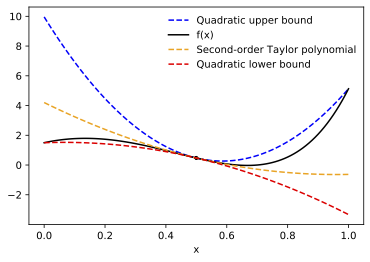
AutoBound: Automatically Bounding Functions

AutoBound is a generalization of automatic differentiation. In addition to computing a Taylor polynomial approximation of a function, it computes upper and lower bounds that are guaranteed to hold over a user-specified trust region.

As an example, here are the quadratic upper and lower bounds AutoBound computes for the function f(x) = 1.5*exp(3*x) - 25*(x**2), centered at 0.5, and valid over the trust region [0, 1].

The code to compute the bounds shown in this plot looks like this (see quickstart):

import autobound.jax as ab
import jax.numpy as jnp

f = lambda x: 1.5*jnp.exp(3*x) - 25*x**2
x0 = .5
trust_region = (0, 1)
# Compute quadratic upper and lower bounds on f.
bounds = ab.taylor_bounds(f, 2)(x0, trust_region)
# bounds.upper(1) == 5.1283045 == f(1)
# bounds.lower(0) == 1.5 == f(0)
# bounds.coefficients == (0.47253323, -4.8324013, (-5.5549355, 28.287888))

These bounds can be used for:

• Computing learning rates that are guaranteed to reduce a loss function
• Upper and lower bounding integrals
• Proving optimality guarantees in global optimization

and more!

Under the hood, AutoBound computes these bounds using an interval arithmetic variant of Taylor-mode automatic differentiation. Accordingly, the memory requirements are linear in the input dimension, and the method is only practical for functions with low-dimensional inputs. A reverse-mode algorithm that efficiently handles high-dimensional inputs is under development.

A detailed description of the AutoBound algorithm can be found in this paper.

Installation

Assuming you have installed pip, you can install this package directly from GitHub with

pip install git+https://github.com/google/autobound.git

or from PyPI with

pip install autobound

You may need to upgrade pip before running these commands.

Limitations

The current code has a few limitations:

• Only JAX-traceable functions can be automatically bounded.
• Many JAX library functions are not yet supported. What is supported is bounding the squared error loss of a multi-layer perceptron or convolutional neural network that uses the jax.nn.sigmoid, jax.nn.softplus, or jax.nn.swish activation functions.
• To compute accurate bounds for deeper neural networks, you may need to use float64 rather than float32.

Citing AutoBound

To cite this repository:

@article{autobound2022,
  title={Automatically Bounding the Taylor Remainder Series: Tighter Bounds and New Applications},
  author={Streeter, Matthew and Dillon, Joshua V},
  journal={arXiv preprint arXiv:2212.11429},
  url = {http://github.com/google/autobound},
  year={2022}
}

This is not an officially supported Google product.