-
Notifications
You must be signed in to change notification settings - Fork 592
A note on data availability and erasure coding
Edit 2018.09.25: see https://arxiv.org/abs/1809.09044 for a paper version of this.
In order to understand the data availability problem, it is best to first start off by understanding the concept of "fraud proofs". Suppose that an attacker makes a block which is invalid in some way (for example, the post-state root is wrong, or some transaction is invalid or mal-formatted). Then, it is possible to create a "fraud proof" that contains the transaction and some Merkle tree data from the state and use it to convince any light client, as well as the blockchain itself, that the block is invalid. Intuitively, one can think of this fraud proof as containing just the parts of the state required to process the block in question, plus some hashes to prove that the parts of the state provided actually do represent the state that the block claims to be building on top of. Verifying the fraud proof involves using the given information to try to actually process the block, and see if there is some error in the processing; if there is, then the block is invalid.
The possibility of fraud proofs theoretically allows light clients to get a nearly-full-client-equivalent assurance that blocks that the client receives are not fraudulent ("nearly", because the mechanism has the additional requirement that the light client is connected to at least some other honest nodes): if a light client receives a block, then it can ask the network if there are any fraud proofs, and if there are not then after some time the light client can assume that the block is valid.
The incentive structure for fraud proofs is simple:
- If someone sends an invalid fraud proof, they lose their entire deposit.
- If someone sends a valid fraud proof, the creator of the invalid block loses their entire deposit, and some small portion goes to the fraud proof creator as a reward.
Although this mechanism is elegant, it contains an important hole: what if an attacker creates a (possibly valid, possibly invalid) block but does not publish 100% of the data? Even if succinct zero knowledge proofs can be used to verify correctness, an attacker getting away with publishing unavailable blocks and getting them included in the chain is still very bad, as such a thing happening denies all other validators the ability to fully calculate the state, or to make blocks that interact with the portion of the state that is no longer accessible. There are also other bad consequences to accepting valid blocks with unpublished data; for example, schemes such as hash locks for atomic cross chain swaps or coin-for-data trading rely on the assumption that data published to the blockchain will be publicly accessible.
Here, fraud proofs are not a solution, because not publishing data is not a uniquely attributable fault - in any scheme where a node ("fisherman") has the ability to "raise the alarm" about some piece of data not being available, if the publisher then publishes the remaining data, all nodes who were not paying attention to that specific piece of data at that exact time cannot determine whether it was the publisher that was maliciously withholding data or whether it was the fisherman that was maliciously making a false alarm.
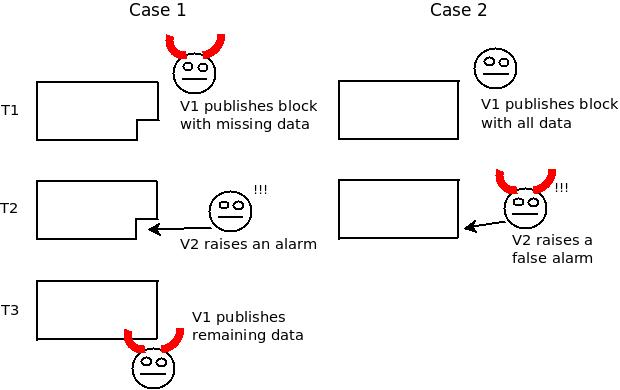
Notice that from the point of view of someone who only checks on the data after T3, case 1 and case 2 are indistinguishable.
This then creates an impossible choice:
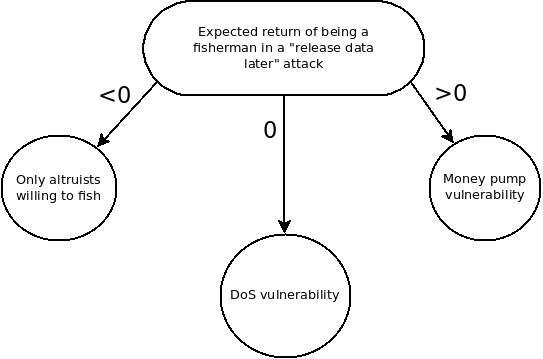
Suppose that an attacker engages in an attack where they withhold data, wait for a fisherman to catch them, and then release the data immediately. In such a scenario, is the reward of the fisherman net positive? If so, malicious fisherman raising false alarms is a money pump vulnerability. Is the reward zero? If so, this is a cost-free DoS vulnerability that can be exploited to force nodes to download all data in the blockchain, nullifying the benefits of light clients or sharding. Is the reward negative? If so, then being a fisherman is an altruistic act, and so an attacker need only economically outlast altruistic fishermen at which point they are then free to include blocks with data unavailable unimpeded.
One natural solution to this is to have light clients all verify data availability of a block before accepting it as valid, but do so probabilistically. A light client might pick twenty random chunks of a block, try to download them from the network (using the Merkle root in the block header to verify each chunk), and only accept the block if all twenty requests get a valid response. If this check passes, and assuming an "honest minority assumption" that there are enough honest users making these checks that the honest users together are making enough requests to download most of the block, a light client knows that with very high probability that the majority of the block is available.
However, there are still very dangerous attacks that could take place from only withholding a few hundred bytes of data, and such an attack would still slip through most clients making such a check. To solve this problem, we use erasure codes. Erasure codes allow a piece of data M chunks long to be expanded into a piece of data N chunks long ("chunks" can be of arbitrary size), such that any M of the N chunks can be used to recover the original data. We require blocks to commit to the Merkle root of this "extended" data, and have light clients probabilistically check that the majority of the extended data is available.
If the majority of the extended data is available, the light client knows that one of three things is true:
- The entire extended data is available, the erasure code is constructed correctly, and the block is valid.
- The entire extended data is available, the erasure code is constructed correctly, but the block is invalid.
- The entire extended data is available, but the erasure code is constructed incorrectly.
In case (1), the block is valid and the light client can accept it. In case (2), it is expected that some other node will quickly construct and relay a fraud proof. In case (3), it is also expected that some other node will quickly construct and relay a specialized kind of fraud proof that shows that the erasure code is constructed incorrectly. If a light client receives no fraud proofs for some time, it will take that as evidence that the block is in fact valid.
See here for sample code implementing all of this logic.
If one uses the simplest kind of Reed-Solomon code, the size of a fraud proof in the above scheme is, unfortunately, equal to the size of the entire erasure code. The fraud proof simply consists of M Merkle proofs; the proof checking algorithm verifies the proofs, then it uses those M chunks to compute the remaining chunks, and it checks whether or not the Merkle root of the full set of chunks is equal to the original Merkle root. If it is not, then the code is malformed.
Here are some approximate statistics for applying a one-dimensional Reed-Solomon code to 256 KB and 1 MB of data, using 256-byte chunks:
- Size of light client proof (256 KB): 20 branches * (256 bytes + 10 Merkle tree intermediate hashes * 32 bytes per hash) = 11520 bytes
- Size of light client proof (1 MB): 20 branches * (256 bytes + 12 Merkle tree intermediate hashes * 32 bytes per hash) = 12800 bytes
- Time spent to encode in C++ (256 KB): 2.4 seconds
- Time spent to encode in C++ (1 MB): 21 seconds
- Time spent to verify fraud proof (256 KB): 2.4 seconds
- Time spent to verify fraud proof (1 MB): 21 seconds
- Size of fraud proof (256 KB): ~256-512 KB
- Size of fraud proof (1 MB): ~1-2 MB
The computation times include partial optimizations; ~3/4 of the Lagrange interpolation is sped up to sub-quadratic runtimes using Karatsuba multiplication, though multi-point evaluations are still done in quadratic time; this is because it was found that sub-quadratic algorithms for multi-point evaluation are both more difficult to implement and had much higher constant factors, and so it was deemed a less worthwhile tradeoff to implement them. The above runtimes also are done on a single core; all algorithms involved are highly parallelizable and highly GPU-friendly, so further speedups are possible.
One can go further by making the erasure code multidimensional. In a simple Reed-Solomon code, the original data is interpreted as a set of points representing the evaluation of a polynomial at x=0, x=1 ... x=M-1; the process of extending the data involves using Lagrange interpolation to compute the coefficients of the polynomial and then evaluating it at points x=M ... x=N-1. We can improve on this by instead interpreting the data as a square, representing the evaluation of a polynomial at (x=0, y=0) ... (x=sqrt(M)-1, y=sqrt(M)-1). The square can then be extended to a bigger square, going up to (x=2*sqrt(M)-1, y=2*sqrt(M)-1). This reduces the computational complexity of computing the proofs as the polynomials involved are lower-degree, and also reduces the size of the fraud proofs.
In such a model, we add some further complexity to the data structures involved. First of all, instead of having a single Merkle root, we now have 4 * sqrt(M) Merkle roots, one for each row and one for each column. Light clients would need to download all of this data as part of a light client proof. For a 1 MB file with 256-byte chunks (ie. 4096 chunks in the original file in a 64x64 shape, so 128x128 in the expanded version), this would consist of 256 32-byte hashes, or 8192 extra bytes in the proof. Additionally, the number of branches required goes up from 20 to 48 to compensate for the fact that the 2D erasure code is more "fragile". On the plus side, the size of a Merkle branch is lower.
A major benefit of this is that the size of a fraud proof is much lower: a fraud proof now consists of M values in a single row or column plus Merkle proofs for these values, and the process of verifying the proof involves "recovering" the missing data from these values, computing the Merkle root, and showing that this does not match the Merkle root provided. Note that the fraud prover has total free choice about whether the Merkle proofs provided come from the Merkle trees for the row or the column; this allows fraud proofs to cover both malformed rows and columns and inconsistencies between the row and column Merkle trees.
We now present the new statistics, still with 256-byte chunks, for 1 MB (4096 chunks) and 4 MB (16384 chunks). Note that these are estimates; the algorithms for doing this in full have not been fully implemented.
- Size of light client proof (1 MB): 48 branches * (256 bytes + 6 Merkle tree intermediate hashes * 32 bytes per hash) + (128 Merkle roots * 32 bytes per hash) = 25600 bytes
- Size of light client proof (4 MB): 48 branches * (256 bytes + 7 Merkle tree intermediate hashes * 32 bytes per hash) + (256 Merkle roots * 32 bytes per hash) = 31232 bytes
- Time spent to encode in C++ (1 MB): 7.5 seconds
- Time spent to encode in C++ (4 MB): 43.45 seconds
- Time spent to verify fraud proof (1 MB): < 0.01 seconds
- Time spent to verify fraud proof (4 MB): < 0.01 seconds
- Maximum size of fraud proof (1 MB): 6 Merkle tree intermediate hashes * 32 bytes per hash * 64 elements = 12288 bytes
- Maximum size of fraud proof (4 MB): 7 Merkle tree intermediate hashes * 32 bytes per hash * 128 elements = 28672 bytes
How could this fit together into a complete mechanism for data availability and fraud proofs in a blockchain?
A simple and generic approach is as follows. Every top-level block would contain a Merkle root of erasure coded data. The data would be the entire data that makes up the top-level block in some canonical serialized form, including the contents of every shard. Whenever there exist parts of a block that might have variable length, either they are padded with zero bytes up to their maximum possible length (eg. as determined by the block size or gas limit), or a table at the start of the encoded data is used to denote the start and end of each chunk.
There would then be two kinds of fraud proof. The first kind is a fraud proof of the erasure code itself, which depends on the specific algorithm used. The second kind is a fraud proof showing that the data committed to in the erasure coded Merkle root does not follow the rules of the protocol. If, for example, the rules of the protocol specify that the bazook should be equal to the sha3 of the concatenation of the kabloog and the mareez, and the canonical encoding of the block places the bazook at bytes 1000...1031, the kabloog at bytes 50000...50999 and the mareez at bytes 55000...55999, then one can make a proof consisting of the Merkle branches from the erasure coded Merkle root pointing to the bazook, kabloog and mareez, and one can verify that the three values do not satisfy the relation that the protocol says they should satisfy.
Sort of but not quite. PoR protocols generally work as follows. Alice creates a file, sends it to Bob, and then Bob proves to Alice using some tricks (that usually also involve erasure coding and random sampling) that he still has the file. Sometimes, Bob needs to prove to Carol instead of Alice, and there are some restrictions on what information can be shared between Alice and Carol. These protocols often involve MACs or in more advanced cases various partially homomorphic schemes including elliptic curves. In all cases, Alice is assumed to be trusted, in the sense that we assume that any "check data" added by Alice was added correctly, that the file actually exists, and that any kind of "public key" given by Alice to Carol was generated correctly.
In our model, the (potential adversary) Bob is themselves the one creating the file. Bob submits some small piece of data (think, the Merkle root of the erasure coded data) to Carol, and Carol is seeking an assurance that the Merkle root actually does represent a piece of data, that it was constructed correctly, and that this data is retrievable. Carol trusts no one except for herself, and the assurance that there exist enough other Carols also making spot checks that between them, they can either find a flaw in the data or they can download the entire file.
A key desired property is consensus - if Carol verification algorithm for some file returns TRUE, and we assume there are enough verifying clients in the network, then with very high probability David will also, perhaps after some time bound based on network latency, return TRUE for the same file; it cannot be possible for different participants to permanently disagree on the result, even if Bob crafts and publishes data maliciously.
There are two major challenges.
- If we simply take the two-dimensional scheme and try to make it higher-dimensional, then the number of intermediate Merkle roots that would go into a light client proof becomes extremely large, and instead of including those Merkle roots directly in the light client proof, we make yet another data availability proof of them, which would then need a much smaller number of Merkle roots.
- If the proofs are extremely large, then we cannot rely on a single node making the entire proof. Instead, we would need to rely on some kind of collaborative generation. However, this makes fault identification harder; if row X does not match with column Y or shaft Z, and the two were made by different validators, how do we tell whose fault it is? This is likely solvable, perhaps by having validators point to a "justification" for the row/column/shaft, eg. a bit mask for which existing values they used, which could then be used to deduce which party was at fault, but this adds complexity to the scheme.
Yes. A proof of proximity is a short proof that can be added to a Merkle root that probabilistically (in the Fiat-Shamir sense) proves that at least some large percentage (eg. 90%) of the data in the Merkle tree is on the same low-degree polynomial. See https://vitalik.ca/general/2017/11/22/starks_part_2.html for a detailed description of how PoPs work.
One can create a proof of proximity that proves that some Merkle root with 2N values is 90% close to a degree-N polynomial, and this proves that there is some unique set of data (N values) that the data is close to. Users can verify this proof, and also randomly download a sample of branches of the tree to probabilistically verify that, for example, at least 80% of the data is available. In such a case, any two users that pass the same test will definitely have at least N * 1.44 values, which they can use to recover the original data (perhaps cancelling out errors with something like the Berlekamp-Welch algorithm), and there is an assurance that the data recovered by those two users will be the same.
One difficulty that this approach introduces is that not every Merkle branch will point to the underlying data, as the proof of proximity can tolerate a small number of faults; hence, proving membership of any specific piece of data would require a proof of proximity augmented with a proof that the value presented by that Merkle branch is on the same low-degree polynomial. So this is ultimately inferior to the further solution described below...
Yes. SNARKs and STARKs can be used to create succinct (ie. O(1)-sized) proofs that the Merkle root of the data was constructed correctly, and at the same time prove that the state transitions executed in the block are valid. This allows us to make the process of verifying a block very conceptually simple.
Suppose that a header is of the form (prev_state_root, tx_root, post_state_root, proof, sig...), where proof is a STARK. The proof would prove that the tx_root is the Merkle tree root of some data, where one part of the data is a set of transactions, and the other parts of the data are a correctly formed erasure code for that data; it would also prove that executing those transactions on top of prev_state_root would result in post_state_root as the final state root hash. Note that to create the STARK, the creator would need to provide all of the Merkle tree nodes accessed as a "witness", but this data does not need to go into the STARK itself.
To verify a block, a client would only need to download the header, verify the STARK, and then randomly sample some Merkle branches of the erasure coded data.
A more advanced mechanism can be created using recursive STARKs (ie. STARKs proving the validity of other STARKs), allowing the erasure coded data to be created collaboratively, solving the second problem mentioned above. Theoretically, the only upper limit to the scalability of such a scheme is the amount of data that nodes around the network are willing to reliably store voluntarily.
Can an attacker not circumvent this scheme by releasing a full unavailable block, but then only releasing individual bits of data as clients query for them?
Kind of, but with limitations. Suppose that a block has 4 MB data, and each light client is making 20 queries for 256 bytes each. If, in the entire network, there are less than 820 light clients, then it is indeed the case that the attacker can do such an attack, and trick every light client into believing the block is available when in reality not enough data was published to reconstruct the whole thing (in reality, you need ~1140 light clients to make up for overlap, and more if the erasure code is two-dimensional). Also, if the erasure code is fraudulent, then the fraud may never be discovered.
Hence, the scheme depends on two honest minority assumptions:
- There exist enough honest light clients that the intersection of their data availability proof requests is overwhemingly likely to be equal to enough of the erasure coded data to recover the whole thing.
- There exist enough honest nodes that will generate and forward fraud proofs if they discover that any part of the erasure code is fraudulent
Now, even if there are more than 1140 honest light clients, an attacker could decide to answer the requests of the first 1000 of them, and then stop responding to requests, thereby tricking a few nodes. This can be overcome by sending each request separately through an anonymizing onion routing network, so that an attacker cannot tell which requests came from the same node. Nodes that partially trust each other (ie. trust each other to probably not be sybils) could also gossip to each other if they get a failure on any of their requests, allowing other nodes to try to make that request themselves; this way, if a block is rejected by a large portion of nodes, it would come to be rejected by all nodes.
It is imperfect, but do note that if the design is constructed correctly many things have to go wrong at once for the scheme to fail. A well-designed scalable data availability verification scheme would have a randomly selected committee of validators sign off on each piece of data, so both the honest majority model and the honest client minority assumption would need to fail for unavailable data to get through. That said, making sure that the data does not spread so thin that the honest client minority assumption becomes an actual concern is perhaps the main scalability limitation that the scheme does have; even if it works well for gigabyte blocks, it would not work well for petabyte blocks.