-
Notifications
You must be signed in to change notification settings - Fork 30
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
* New NLSolversBase
- Loading branch information
Showing
11 changed files
with
725 additions
and
278 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -1,17 +1,152 @@ | ||
| # NLSolversBase | ||
| NLSolversBase.jl | ||
| ======== | ||
|
|
||
| NLSolversBase is the core, common dependency of several [JuliaNLSolvers](https://github.com/JuliaNLSolvers) packages. Currently, it aims at establishing common ground for [Optim.jl](https://github.com/JuliaNLSolvers/Optim.jl) and [LineSearches.jl](https://github.com/JuliaNLSolvers/LineSearches.jl), but [NLsolve.jl](https://github.com/JuliaNLSolvers/NLsolve.jl) will eventually also depend on this package. The common ground is mainly the types used to hold objectives and information about the objectives, and an interface to interact with these types. | ||
| Base functionality for optimization and solving systems of equations in Julia. | ||
|
|
||
| Travis-CI | ||
| NLSolversBase.jl is the core, common dependency of several packages in the [JuliaNLSolvers](https://julianlsolvers.github.io) family. | ||
|
|
||
| [](https://travis-ci.org/JuliaNLSolvers/NLSolversBase.jl) | ||
|
|
||
| Package evaluator | ||
| | **PackageEvaluator** |**Build Status** | | ||
| |:-------------------------------:|:-------------------------------------------------:| | ||
| | [![][pkg-0.4-img]][pkg-0.4-url] | [![Build Status][build-img]][build-url] | | ||
| | [![][pkg-0.5-img]][pkg-0.5-url] | [![Codecov branch][cov-img]][cov-url] | | ||
| | [![][pkg-0.6-img]][pkg-0.6-url] | [![Coverage Status][coveralls-img]][coveralls-url]| | ||
|
|
||
| [](http://pkg.julialang.org/?pkg=NLSolversBase&ver=0.5) | ||
| [](http://pkg.julialang.org/?pkg=NLSolversBase&ver=0.6) | ||
|
|
||
| Code coverage | ||
| # Purpose | ||
|
|
||
| [](https://coveralls.io/github/JuliaNLSolvers/NLSolversBase.jl?branch=master) | ||
| [](http://codecov.io/github/pkofod/NLSolversBase.jl?branch=master) | ||
| The package aims at establishing common ground for [Optim.jl](https://github.com/JuliaNLSolvers/Optim.jl), [LineSearches.jl](https://github.com/JuliaNLSolvers/LineSearches.jl), and [NLsolve.jl](https://github.com/JuliaNLSolvers/NLsolve.jl). The common ground is mainly the types used to hold objective related callables, information about the objectives, and an interface to interact with these types. | ||
|
|
||
| ## NDifferentiable | ||
| There are currently three main types: `NonDifferentiable`, `OnceDifferentiable`, and `TwiceDifferentiable`. There's also a more experimental `TwiceDifferentiableHV` for optimization algorithms that use Hessian-vector products. An `NDifferentiable` instance can be used to hold relevant functions for | ||
|
|
||
| - Optimization:  | ||
| - Solving systems of equations: 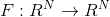 | ||
|
|
||
| The words in front of `Differentiable` in the type names (`Non`, `Once`, `Twice`) are not meant to indicate and specific classification of the function as such, but more the requirement of the algorithms used. | ||
|
|
||
| ## Examples | ||
| #### Optimization | ||
| Say we want to minimize the Hosaki test function | ||
|
|
||
|  | ||
|
|
||
| The relevant functions are coded in Julia as | ||
| ```julia | ||
| function f(x) | ||
| a = (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) | ||
| return a * x[2]^2 * exp(-x[2]) | ||
| end | ||
|
|
||
| function g!(G, x) | ||
| G[1] = (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8)* x[2]^2 * exp(-x[2]) | ||
| G[2] = 2.0 * (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2] * exp(-x[2]) - (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2]^2 * exp(-x[2]) | ||
| end | ||
|
|
||
| function fg!(G, x) | ||
| g!(G, x) | ||
| f(x) | ||
| end | ||
|
|
||
| function h!(H, x) | ||
| H[1, 1] = (3.0 * x[1]^2 - 14.0 * x[1] + 14.0) * x[2]^2 * exp(-x[2]) | ||
| H[1, 2] = 2.0 * (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2] * exp(-x[2]) - (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2]^2 * exp(-x[2]) | ||
| H[2, 1] = 2.0 * (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2] * exp(-x[2]) - (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2]^2 * exp(-x[2]) | ||
| H[2, 2] = 2.0 * (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * exp(-x[2]) - 4.0 * ( 1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2] * exp(-x[2]) + (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2]^2 * exp(-x[2]) | ||
| end | ||
| ``` | ||
| The `NDifferentiable` interface can be used as shown below to create various objectives: | ||
| ```julia | ||
| x = zeros(4) | ||
| nd = NonDifferentiable(f, x) | ||
| od = OnceDifferentiable(f, g!, x) | ||
| odfg = OnceDifferentiable(f, g!, fg! x) | ||
| td1 = Twicedifferentiable(f, g!, h! x) | ||
| tdfg = Twicedifferentiable(f, g!, fg!, h! x) | ||
| ``` | ||
| #### Multivalued objective | ||
| If we consider the gradient of the Himmelblau function above, we can try to solve  without caring about the objective value. Then we can still create `NDifferentiable`s, but we need to specify the cache to hold the value of 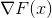. Currently, the only relevant ones are `NonDifferentiable` and `OnceDifferentiable`. `TwiceDifferentiable` could be used for higher order (tensor) methods, though they are rarely worth the cost. The relevant functions coded in Julia are: | ||
|
|
||
| ```julia | ||
| function f!(F, x) | ||
| F[1] = (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8)* x[2]^2 * exp(-x[2]) | ||
| F[2] = 2.0 * (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2] * exp(-x[2]) - (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2]^2 * exp(-x[2]) | ||
| end | ||
|
|
||
| function j!(J, x) | ||
| J[1, 1] = (3.0 * x[1]^2 - 14.0 * x[1] + 14.0) * x[2]^2 * exp(-x[2]) | ||
| J[1, 2] = 2.0 * (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2] * exp(-x[2]) - (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2]^2 * exp(-x[2]) | ||
| J[2, 1] = 2.0 * (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2] * exp(-x[2]) - (x[1]^3 - 7.0 * x[1]^2 + 14.0 * x[1] - 8.0) * x[2]^2 * exp(-x[2]) | ||
| J[2, 2] = 2.0 * (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * exp(-x[2]) - 4.0 * ( 1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2] * exp(-x[2]) + (1.0 - 8.0 * x[1] + 7.0 * x[1]^2 - (7.0 / 3.0) * x[1]^3 + (1.0 / 4.0) * x[1]^4) * x[2]^2 * exp(-x[2]) | ||
| end | ||
|
|
||
| function fj!(F, G, x) | ||
| g!(G, x) | ||
| f!(F, x) | ||
| end | ||
| ``` | ||
| The `NDifferentiable` interface can be used as shown below to create various objectives: | ||
| ```julia | ||
| x = zeros(4) | ||
| F = zeros(4) | ||
| nd = NonDifferentiable(f!, x, F) | ||
| od = OnceDifferentiable(f!, j!, x, F) | ||
| odfj = OnceDifferentiable(f!, j!, fj! x, F) | ||
| ``` | ||
|
|
||
| ## Interface | ||
|
|
||
| To extract information about the objective, and to update given some input, we provide a function based interface. For all purposes it should be possible to use a function to extract/update information, and no field access should be necessary. Actually, we proactively discourage it, as it makes it much more difficult to make changes in the future. | ||
|
|
||
| ### Single-valued objectives | ||
| To retrieve relevant information about single-valued functions, the following functions are available where applicable: | ||
| ```julia | ||
| # obj is the objective function defined as shown above | ||
| value(df) # return the objective evaluated at df.x_f | ||
| gradient(df) # return the gradient evaluated at df.x_df | ||
| gradient(df, i) # return the gradient evaluated at df.x_df | ||
| hessian(df) # return the hessian evaluated at df.x_h | ||
| ``` | ||
| To update the various quantities, use: | ||
| ```julia | ||
| # obj is the objective function defined as shown above | ||
| value!(df, x) # update the objective if !(df.x_f==x) and set df.x_f to x | ||
| value!!(df, x) # update the objective and set df.x_f to x | ||
| gradient!(df, x) # update the gradient if !(df.x_df==x) and set df.x_df to x | ||
| gradient!!(df, x) # update the gradient and set df.x_df to x | ||
| hessian!(df,x) # update the hessian if !(df.x_df==x) and set df.x_h to x | ||
| hessian!!(df,x) # update the hessian and set df.x_h to x | ||
| ``` | ||
|
|
||
| ### Multivalued | ||
| To retrieve relevant information about multivalued functions, the following functions are available where applicable: | ||
| ```julia | ||
| # obj is the objective function defined as shown above | ||
| value(df) # return the objective evaluated at df.x_f | ||
| jacobian(df) # return the jacobian evaluated at df.x_df | ||
| jacobian(df) # return the jacobian evaluated at df.x_df | ||
| ``` | ||
| To update the various quantities, use: | ||
| ```julia | ||
| # obj is the objective function defined as shown above | ||
| value!(df, x) # update the objective if !(df.x_f==x) and set df.x_f to x | ||
| value!!(df, x) # update the objective and set df.x_f to x | ||
| jacobian!(df, x) # update the jacobian if !(df.x_df==x) and set df.x_df to x | ||
| jacobian!!(df, x) # update the jacobian and set df.x_df to x | ||
| ``` | ||
|
|
||
| [build-img]: https://travis-ci.org/JuliaNLSolvers/NLSolversBase.jl.svg?branch=master | ||
| [build-url]: https://travis-ci.org/JuliaNLSolvers/NLSolversBase.jl | ||
|
|
||
| [pkg-0.4-img]: http://pkg.julialang.org/badges/NLSolversBase_0.4.svg | ||
| [pkg-0.4-url]: http://pkg.julialang.org/?pkg=NLSolversBase&ver=0.4 | ||
| [pkg-0.5-img]: http://pkg.julialang.org/badges/NLSolversBase_0.5.svg | ||
| [pkg-0.5-url]: http://pkg.julialang.org/?pkg=NLSolversBase&ver=0.5 | ||
| [pkg-0.6-img]: http://pkg.julialang.org/badges/NLSolversBase_0.6.svg | ||
| [pkg-0.6-url]: http://pkg.julialang.org/?pkg=NLSolversBase&ver=0.6 | ||
|
|
||
| [cov-img]: http://codecov.io/github/JuliaNLSolvers/NLSolversBase.jl/coverage.svg?branch=master | ||
| [cov-url]: http://codecov.io/github/pkofod/NLSolversBase.jl?branch=master | ||
|
|
||
| [coveralls-img]: https://coveralls.io/repos/JuliaNLSolvers/NLSolversBase.jl/badge.svg?branch=master&service=github | ||
| [coveralls-url]: https://coveralls.io/github/JuliaNLSolvers/NLSolversBase.jl?branch=master |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -1,62 +1,113 @@ | ||
| function _unchecked_value!(obj, x) | ||
| function value!!(obj::AbstractObjective, x) | ||
| obj.f_calls .+= 1 | ||
| copy!(obj.last_x_f, x) | ||
| obj.f_x = obj.f(real_to_complex(obj, x)) | ||
| copy!(obj.x_f, x) | ||
| obj.F = obj.f(real_to_complex(obj, x)) | ||
| end | ||
| function value(obj, x) | ||
| if x != obj.last_x_f | ||
| function value(obj::AbstractObjective, x) | ||
| if x != obj.x_f | ||
| obj.f_calls .+= 1 | ||
| return obj.f(real_to_complex(obj,x)) | ||
| end | ||
| obj.f_x | ||
| obj.F | ||
| end | ||
| function value!(obj, x) | ||
| if x != obj.last_x_f | ||
| _unchecked_value!(obj, x) | ||
| function value!(obj::AbstractObjective, x) | ||
| if x != obj.x_f | ||
| value!!(obj, x) | ||
| end | ||
| obj.f_x | ||
| obj.F | ||
| end | ||
|
|
||
|
|
||
| function _unchecked_gradient!(obj, x) | ||
| obj.g_calls .+= 1 | ||
| copy!(obj.last_x_g, x) | ||
| obj.g!(real_to_complex(obj, obj.g), real_to_complex(obj, x)) | ||
| function gradient(obj::AbstractObjective, x) | ||
| if x != obj.x_df | ||
| tmp = copy(obj.DF) | ||
| gradient!!(obj, x) | ||
| newdf = copy(obj.DF) | ||
| copy!(obj.DF, tmp) | ||
| return newdf | ||
| end | ||
| obj.DF | ||
| end | ||
| function gradient!(obj::AbstractObjective, x) | ||
| if x != obj.last_x_g | ||
| _unchecked_gradient!(obj, x) | ||
| if x != obj.x_df | ||
| gradient!!(obj, x) | ||
| end | ||
| end | ||
| function gradient!!(obj::AbstractObjective, x) | ||
| obj.df_calls .+= 1 | ||
| copy!(obj.x_df, x) | ||
| obj.df(real_to_complex(obj, obj.DF), real_to_complex(obj, x)) | ||
| end | ||
|
|
||
| function value_gradient!(obj::AbstractObjective, x) | ||
| if x != obj.last_x_f && x != obj.last_x_g | ||
| obj.f_calls .+= 1 | ||
| obj.g_calls .+= 1 | ||
| copy!(obj.last_x_f, x) | ||
| copy!(obj.last_x_g, x) | ||
| obj.f_x = obj.fg!(real_to_complex(obj, obj.g), real_to_complex(obj, x)) | ||
| elseif x != obj.last_x_f | ||
| _unchecked_value!(obj, x) | ||
| elseif x != obj.last_x_g | ||
| _unchecked_gradient!(obj, x) | ||
| if x != obj.x_f && x != obj.x_df | ||
| value_gradient!!(obj, x) | ||
| elseif x != obj.x_f | ||
| value!!(obj, x) | ||
| elseif x != obj.x_df | ||
| gradient!!(obj, x) | ||
| end | ||
| obj.f_x | ||
| obj.F | ||
| end | ||
|
|
||
| function _unchecked_hessian!(obj::AbstractObjective, x) | ||
| obj.h_calls .+= 1 | ||
| copy!(obj.last_x_h, x) | ||
| obj.h!(obj.H, x) | ||
| function value_gradient!!(obj::AbstractObjective, x) | ||
| obj.f_calls .+= 1 | ||
| obj.df_calls .+= 1 | ||
| copy!(obj.x_f, x) | ||
| copy!(obj.x_df, x) | ||
| obj.F = obj.fdf(real_to_complex(obj, obj.DF), real_to_complex(obj, x)) | ||
| end | ||
|
|
||
| function hessian!(obj::AbstractObjective, x) | ||
| if x != obj.last_x_h | ||
| _unchecked_hessian!(obj, x) | ||
| if x != obj.x_h | ||
| hessian!!(obj, x) | ||
| end | ||
| end | ||
| function hessian!!(obj::AbstractObjective, x) | ||
| obj.h_calls .+= 1 | ||
| copy!(obj.x_h, x) | ||
| obj.h(obj.H, x) | ||
| end | ||
|
|
||
| # Getters are without ! and accept only an objective and index or just an objective | ||
| value(obj::AbstractObjective) = obj.f_x | ||
| gradient(obj::AbstractObjective) = obj.g | ||
| gradient(obj::AbstractObjective, i::Integer) = obj.g[i] | ||
| value(obj::AbstractObjective) = obj.F | ||
| gradient(obj::AbstractObjective) = obj.DF | ||
| jacobian(obj::AbstractObjective) = gradient(obj) | ||
| gradient(obj::AbstractObjective, i::Integer) = obj.DF[i] | ||
| hessian(obj::AbstractObjective) = obj.H | ||
|
|
||
| value_jacobian!(obj, x) = value_jacobian!(obj, obj.F, obj.DF, x) | ||
| function value_jacobian!(obj, F, DF, x) | ||
| if x != obj.x_f && x != obj.x_df | ||
| value_jacobian!!(obj, F, DF, x) | ||
| elseif x != obj.x_f | ||
| value!!(obj, x) | ||
| elseif x != obj.x_df | ||
| jacobian!!(obj, x) | ||
| end | ||
| end | ||
| value_jacobian!!(obj, x) = value_jacobian!!(obj, obj.F, obj.DF, x) | ||
| function value_jacobian!!(obj, F, J, x) | ||
| obj.fdf(F, J, x) | ||
| copy!(obj.x_f, x) | ||
| copy!(obj.x_df, x) | ||
| obj.f_calls .+= 1 | ||
| obj.df_calls .+= 1 | ||
| end | ||
|
|
||
| function jacobian!(obj, x) | ||
| if x != obj.x_df | ||
| jacobian!!(obj, x) | ||
| end | ||
| end | ||
| function jacobian!!(obj, x) | ||
| obj.df(obj.DF, x) | ||
| copy!(obj.x_df, x) | ||
| obj.df_calls .+= 1 | ||
| end | ||
|
|
||
| value!!(obj::NonDifferentiable{TF, TX, Tcplx}, x) where {TF<:AbstractArray, TX, Tcplx} = value!!(obj, obj.F, x) | ||
| value!!(obj::OnceDifferentiable{TF, TDF, TX, Tcplx}, x) where {TF<:AbstractArray, TDF, TX, Tcplx} = value!!(obj, obj.F, x) | ||
| function value!!(obj, F, x) | ||
| obj.f(F, x) | ||
| copy!(obj.x_f, x) | ||
| obj.f_calls .+= 1 | ||
| end |
Oops, something went wrong.