DDE too stiff? radau method required?

[AlexNascou]

Hi Everyone,
The following is a question I recently asked on Julia Discourse (https://discourse.julialang.org/t/dde-too-stiff-required-tolerances-are-too-slow/52259) about an issue solving a very stiff set of DDEs. I found some improvement by tweaking the solver options (e.g., specifying dtstops = initTauU and dtmax = 0.1 ), but Chris thought this might require a radau method so I'm opening this issue in case someone wants to tackle it and use this as a benchmark problem. Any help is greatly appreciated!

Original question:

I have a system of DDEs that model host-parasite dynamics in a seasonal environment and I am having some issues because (I think) the equations are so stiff. Basically, when the number of hosts S is too high (> about 500) I have to lower the solver tolerances so much that it becomes prohibitively slow (I need S up to about a 4e6). I believe the low tolerances are required because u[1] decreases to zero so rapidly when S is high that the history function (W_past) just returns zero, which makes matU = 0.0 and therefore u[3] stays at 0.0 (i.e., no infective larvae develop). It may be the case that I just have to use low tolerances and run the simulation for hours and hours, but if anyone has any suggestions to make this work without having to lower the tolerances too much I would be very grateful. I tried several different stiff solvers (Rosenbrock23, Rodas3,4,4P&5, etc.) but without any great success. Maybe some way of adjusting the step size or addressing the discontinuity is possible? Any other general performance tips are also appreciated.

Here is a stripped down MWE:

using QuadGK, Roots, DelayDiffEq, Plots

#parameters

const Temp0K = 15+273.15;
const k = 8.62 * 10^(-5);
const S = 100.0         #Host density

const mu_W_a = 0.0186;
const mu_W_E = 0.87;
const mu_W_EH = 5.0*mu_W_E;
const mu_W_TH = 289.65;
const Phi_a = 0.024;
const Phi_E = 0.46;

const mu_U_a = 0.0001;
const mu_U_E = 0.87;
const mu_U_EH = 5.0*mu_U_E;
const mu_U_TH = 289.65;

const tauU_a = 25.1;
const tauU_E = 0.87;
const tauU_EL = 5.0*tauU_E;
const tauU_TL = 282.0218;

#Development function

function g_U(T)
    tmp = 1 / max(TempKstop, T)
    1 / (tauU_a * exp((tauU_E/k) * (tmp - (1 / Temp0K))) *
      (1 + exp((tauU_EL / k) * (tmp - (1 / tauU_TL)))))
end

function mu_W(T)
  tmp = 1 / max(TempKstop, T)
  mu_W_a * exp((-mu_W_E/k)*((tmp)-(1/Temp0K))) * (1 + exp((mu_W_EH/k)*((-tmp)+(1/mu_W_TH)))); #L1 mort
end

function mu_U(T)
  tmp = 1 / max(TempKstop, T)
  mu_U = mu_U_a * exp((-mu_U_E/k)*((tmp)-(1/Temp0K))) * (1 + exp((mu_U_EH/k)*((-tmp)+(1/mu_U_TH)))); #U mort
end

function Phi(T)
  tmp = 1 / max(TempKstop, T)
  Phi = Phi_a * exp((-Phi_E/k)*((tmp)-(1/Temp0K))); #W penetration into slugs
end


function Re_MWE(du,u,h,p,t)
  #State variables
   W = u[1]; U = u[2]; I = u[3]; DU1 = u[4]; tauU = u[5];

   # History calculations
   ucache = h(p, t - tauU)
   W_past = ucache[1]
   U_past = ucache[2]

   # Compute temperature
   T = Temp(t)
   T_past = Temp(t - tauU)

   # Preliminary calculations
   gU_ratio = g_U(T) / g_U(T_past)
   matW = Phi(T) * S * W #Maturation rate of W
   matU = Phi(T_past) * S * W_past * DU1 * gU_ratio

 #Model

   du[1] =  - mu_W(T) * W - matW                        #W) Free-living L1s
   du[2] = matW - U * mu_U(T) - matU                    #U) Uninfective larvae
   du[3] = matU                                         #I) Infective larvae
   du[4] = DU1 * (mu_U(T_past) * U_past / S * gU_ratio - mu_U(T) * U / S) #Survival probability through delay period
   du[5] = 1 - gU_ratio                                 #tauU) Change in delay duration
 nothing
 end

 #Setup simualation

 #Initial conditions and history
   const InitW = 1.0;
   const InitU = 0.0;
   const InitI = 0.0;

function DySimulate1(alg, tstart, tfin, tol)
        gint(u) = quadgk(g_U ∘ Temp, tstart - u, tstart)[1]
        initTauU = [fzero(u -> gint(u) - p, [0.001, 5000]) for p in [1.0]][1] #Initial lag for each day (where guadgk = 1.0)
        mUint = exp(-(quadgk(mu_U ∘ Temp, tstart-initTauU, tstart)[1]))

        DUinit = mUint
        DUhist = DUinit
        u0 = [InitW, InitU, InitI, DUinit,initTauU]
        h(p,t) = [0.0, 0.0, 0.0, DUhist, initTauU]
        tspan = (tstart, tfin+tstart)

        # Declare dependent lags
        probDynSea = DDEProblem(Re_MWE, u0, h, tspan;
                              dependent_lags = ((u, p, t) -> u[5],))

      solDynSimpSea = solve(probDynSea,alg;  isoutofdomain=(u,p,t) -> any(x -> x < 0.0, u), abstol = tol, reltol = tol)#, save_idxs = 3)
      #solDynSimpSea = solve(probDynSea,alg; dtmax = 0.1, tstops = [initTauU], isoutofdomain=(u,p,t) -> any(x -> x < 0.0, u), abstol = tol, reltol = tol)#, save_idxs = 3)

end

alg = MethodOfSteps(Rosenbrock23())
# alg = MethodOfSteps(Rosenbrock32())
# alg = MethodOfSteps(Rodas4P())
# alg = MethodOfSteps(Rodas4())
# alg = MethodOfSteps(Rodas5())
# alg = MethodOfSteps(TRBDF2())
# alg = MethodOfSteps(KenCarp4())

#Temperature function
const c_K = 263.0; #Mean annual temperature (Kelvins)
const d_K = 0.66478 * c_K + -153.14
const t0 = -1.6962 * c_K +551.43
const TempKstop = 273.15-0.0
Temp(t) = c_K + d_K * sin((t-t0)*2*pi/365);

MWEanswer = DySimulate1(alg,1.0,365.0*2, 1e-4)
p = plot(MWEanswer, vars = (0,[3]))
# scatter!(p,MWEanswer.t, MWEanswer.u)
# p

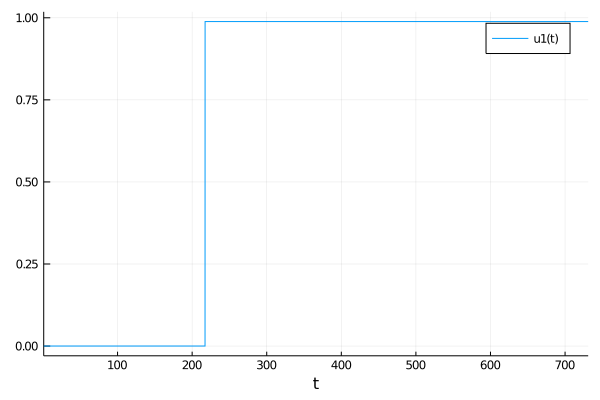
When both the solver tolerances are tol = 1e-4 and S = 100.0 then I get this:

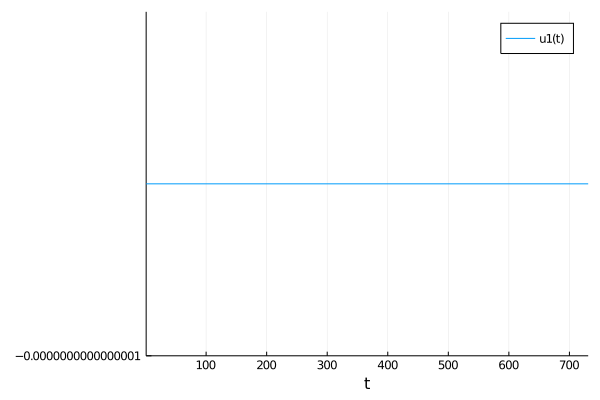
But when tol = 1e-4 and S = 700.0 I get this:

Once I lower the tolerances to tol = 1e-6 with S = 700.0 it works again, but is much much slower and requires larger maxiters. However, with my full model this approach is just too slow, I end up needing to go at least 1e-10 to get anything other than the flat line. I hope I've explained my problem clearly. Thanks.

[devmotion]

I don't have access to a computer right now but two initial observations:

• I'm wondering if you specified tstops and d_didcontinuities incorrectly - the name initTauU indicates that it is an initial delay. However, I assume it would be more important to specify the discontinuity at t > 200.
• I'm wondering if there are some non-DDE related numerical problems here. There are many exp(-...) expressions which makes me think if these quantities should be handled in log space, and maybe only exponentiated at a later stage. More generally, maybe it would be good to transform the variables.

[AlexNascou]

Excellent suggestions. I'll give it a try when I get a chance and report back.

[AlexNascou]

Sorry for the delay in getting back. I looked at the location of the discontinuity again and you're right, it doesn't correspond to initTauU. I'm not sure why that is the case, I thought they would be the same. I will have to investigate that further. Regardless, I found the discontinuity to occur at d_discontinuities = 217.319412. This helps things a bit, and rodas5 now works the best with this specified. However, I still can't go above ~S = 10000.0.

I have yet to transform the variables as you suggested. I'm not exactly sure where you would log and where you would exponentiate. Would you log transform the functions (e.g., g_U()) and then exponentiate them at the beginning of Re_MWE? Or would you need to transform the solution? I start to get issues with the integral gint(u) when working in log space. I will work on it.

[ChrisRackauckas]

At a certain point, you do just need to lower the tolerance to have enough stability on a hard enough problem.

[AlexNascou]

I played around more with the tolerances and dtmax and I now have it working very well. I still find the behaviour a bit strange however. Using Rodas5, I can systematically increase the value of S (e.g., from 10000.0 to 1000000.0) and make it work by lowering the tolerances and trying dtmax = 1 or dtmax = 10 back and forth, and some combination will work (and in just a few seconds!) For example, the following settings work: S = 50000.0, tol = 1e-16, dtmax = 10, S = 500000.0, tol = 1e-18, dtmax = 10 and S = 1000000.0, tol = 1e-18, dtmax = 1, but other combinations of tol and dtmax won't. There doesn't seem to be any rhyme or reason for what works, and it seems strange that dtmax that large (1 or 10) should work but not dtmax = 0.01 or 0.001. Does any of that make sense to you? Or is it a red flag that there are some issues with the code or model? (I wasn't able to figure out how to log transform the variables, but it might still be worth a try. I will have to read up on log transforming odes).

[ChrisRackauckas]

I think it mostly comes down to hitting the discontinuity right. The closer it accidentally gets to some of the discontinuities, the easier the integration is. That would look pretty random.