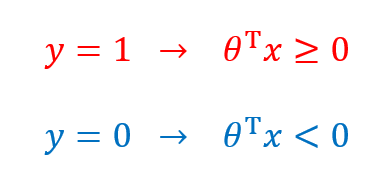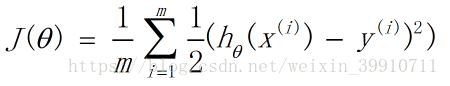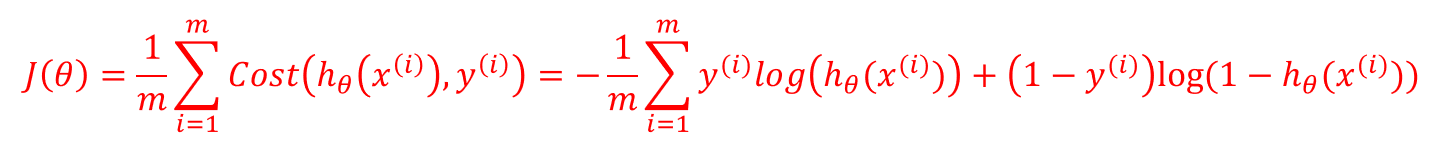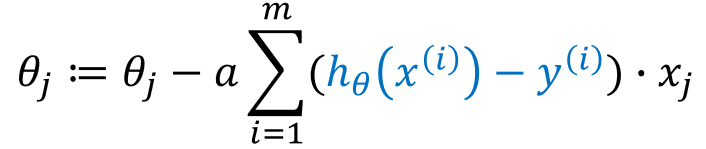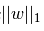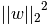第 3 章 图像分类
作者: 张伟 (Charmve)
日期: 2021/04/29
- 第 3 章 图像分类
- 3.1 数据驱动方法
- 3.1.1 语义上的差别
- 3.1.2 图像分类任务面临着许多挑战
- 3.1.3 数据驱动的方法
- 3.2 k 最近邻算法
- 3.2.1 k 近邻模型
- 3.2.2 k 近邻模型三个基本要素
- 3.2.3 KNN算法的决策过程
- 3.2.4 k 近邻算法Python实现
- 小结
- 参考文献
- 3.3 支持向量机
- 3.3.1 概述
- 3.3.2 线性支持向量机
- 3.3.3 从零开始实现支持向量机
- 3.3.4 支持向量机的简洁实现
- 3.4 逻辑回归 LR
- 3.5 实战项目 3 - 表情识别
- 3.6 实战项目 4 - 使用卷积神经网络对CIFAR10图片进行分类
- 小结
- 参考文献
- 3.1 数据驱动方法
机器学习模型大致分为预测模型和分类模型,而分类又分为线性和非线性两类。
| 线性分类器 | 非线性分类器 | |
|---|---|---|
| 概念 | 模型是参数的线性函数,分类平面是(超)平面; | 模型分界面可以是曲面或者超平面的组合; |
| 典型例子 | 感知机,LDA,逻辑斯特回归,SVM(线性核); | 朴素贝叶斯(有文章说这个本质是线性的,http://dataunion.org/12344.html ),kNN,决策树,SVM(非线性核) |
当你的目标变量是分类变量时,才会考虑逻辑回归,并且主要用于两分类问题。
LR 模型可以被认为就是一个被Sigmoid函数(logistic方程)所归一化后的线性回归模型!
逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,使得逻辑回归模型成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。
看了很多博主和相关参考书,他们直接上来就给函数,对于像我这样刚开始学习Machine Learning的VegetableBird来讲,我还是不太愿意从一开始就从公式推导开始。
那我从回归思想讲起。回归是一种极易理解的模型,就相当于y=f(x),表明自变量x与因变量y的关系。最常见问题有如医生治病时的望、闻、问、切,之后判定病人是否生病或生了什么病,其中的望闻问切就是获取自变量x,即特征数据,判断是否生病就相当于获取因变量y,即预测分类。
最简单的回归是线性回归,在此借用Andrew NG的讲义,有如图1.a所示,X为数据点——肿瘤的大小,Y为观测值——是否是恶性肿瘤。通过构建线性回归模型,如hθ(x)所示,构建线性回归模型后,即可以根据肿瘤大小,预测是否为恶性肿瘤hθ(x)≥.05为恶性,hθ(x)<0.5为良性。
图1 线性回归示例
然而线性回归的鲁棒性很差,例如在图1.b的数据集上建立回归,因最右边噪点的存在,使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致,而分类范围,需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型,其回归方程与回归曲线如图2所示。逻辑曲线在z=0时,十分敏感,在z>>0或z<<0处,都不敏感,将预测值限定为(0,1)。
图2 逻辑方程与逻辑曲线逻辑回归其实仅为在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,逻辑回归成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。
对于多元逻辑回归,可用如下公式似合分类,其中公式(4)的变换,将在逻辑回归模型参数估计时,化简公式带来很多益处,y={0,1}为分类结果。
对于训练数据集,特征数据x={x1, x2, … , xm}和对应的分类数据y={y1, y2, … , ym}。构建逻辑回归模型f(θ),最典型的构建方法便是应用极大似然估计。首先,对于单个样本,其后验概率为:
那么,极大似然函数为:
log似然是:
首先来解释一下P(y=1|x,θ)表示的是啥?它表示的就是将因变量预测成1(阳性)的概率,具体来说它所要表达的是在给定x条件下事件y发生的条件概率,而是该条件概率的参数。将它分解一下:
(1)式就是我们介绍的线性回归的假设函数,那(2)式就是我们的Sigmoid函数啦。
由于线性回归在整个实数域内敏感度一致,而分类范围需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型,其回归方程与回归曲线如下图所示。逻辑曲线在z=0时,十分敏感,在z>>0或z<<0处,都不敏感,将预测值限定为(0,1)。为什么会用Sigmoid函数?因为它引入了非线性映射,将线性回归值域[-∞,+∞]映射到0-1之间,有助于直观的做出预测类型的判断:大于等于0.5表示阳性,小于0.5表示阴性。
其实,从本质来说:在分类情况下,经过学习后的LR分类器其实就是一组权值θ,当有测试样本输入时,这组权值与测试数据按照加权得到 $$ h_θ(x) =θ_0 +θ_1x_1+θ_2x_2+θ_3x_3+...+θ_nx_n $$
这里的x1+x2+...xn就是每个测试样本的n个特征值。之后在按照Sigmoid函数的形式求出P(y=1|x,θ),从而去判断每个测试样本所属的类别。
由此看见,LR模型学习最关键的问题就是研究如何求解这组权值!
在LR模型中我们知道:当假设函数,即,此时我们预测成正类;反之预测为负类。由图来看,我们可以得到更加清晰的认识。下图为Sigmoid函数,也是LR的外层函数。我们看到当时,此时(即内层函数),然而此时也正是将y预测为1的时候;同理,我们可以得出内层函数时,我们将其预测成0(即负类)。
逻辑回归的假设函数可以表示为 $$ h_θ(x) = θ^Tx g(z) = \frac{1}{1+e^{-θ^Tz}} $$
,于是我们得到了这样的关系式:
下面再举一个例子,假设我们有许多样本,并在图中表示出来了,并且假设我们已经通过某种方法求出了LR模型的参数(如下图)。
而x1+x2 =3 我们再图像上画出得到:
这时,直线上方所有样本都是正样本y=1,直线下方所有样本都是负样本y=0。因此我们可以把这条直线成为决策边界。
同理,对于非线性可分的情况,我们只需要引入多项式特征就可以很好的去做分类预测,如下图:
值得注意的一点,决策边界并不是训练集的属性,而是假设本身和参数的属性。因为训练集不可以定义决策边界,它只负责拟合参数;而只有参数确定了,决策边界才得以确定。
前面我们介绍线性回归模型时,给出了线性回归的代价函数的形式(误差平方和函数),具体形式如下:
这里我们想到逻辑回归也可以视为一个广义的线性模型,那么线性模型中应用最广泛的代价函数-误差平方和函数,可不可以应用到逻辑回归呢?首先告诉你答案:是不可以的! 那么为什么呢? 这是因为LR的假设函数的外层函数是Sigmoid函数,Sigmoid函数是一个复杂的非线性函数,这就使得我们将逻辑回归的假设函数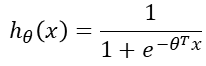
这样的函数拥有多个局部极小值,这就会使得我们在使用梯度下降法求解函数最小值时,所得到的结果并非总是全局最小,而有更大的可能得到的是局部最小值。这样解释应该理解了吧。
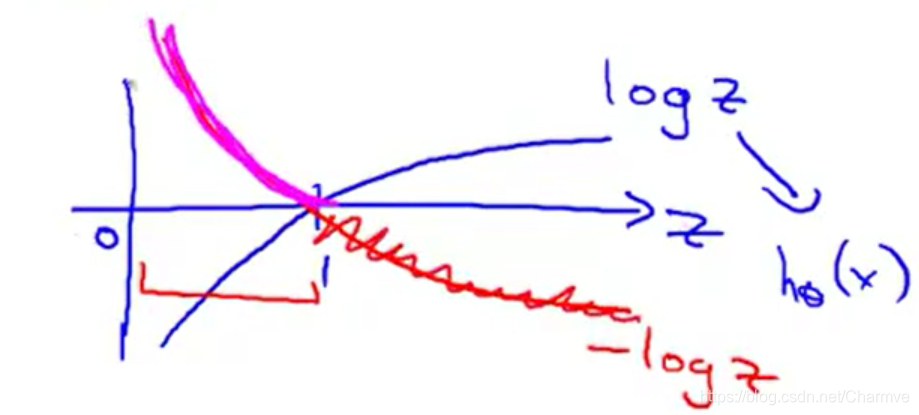
虽然前面的解释否定了我们猜想,但是也给我们指明了思路,那就是我们现在要做的就是为LR找到一个凸的代价函数! 在逻辑回归中,我们最常用的损失函数为对数损失函数,对数损失函数可以为LR提供一个凸的代价函数,有利于使用梯度下降对参数求解。为什么对数函数可以做到这点呢? 我们先看一下对数函数的图像:
蓝色的曲线表示的是对数函数的图像,红色的曲线表示的是负对数-logz的图像,该图像在0-1区间上有一个很好的性质,如图粉红色曲线部分。在0-1区间上当z=1时,函数值为0,而z=0时,函数值为无穷大。这就可以和代价函数联系起来,在预测分类中当算法预测正确其代价函数应该为0;当预测错误,我们就应该用一个很大代价(无穷大)来惩罚我们的学习算法,使其不要轻易预测错误。这个函数很符合我们选择代价函数的要求,因此可以试着将其应用于LR中。对数损失在LR中表现形式如下:
对于代价函数Cost的这两种情况:
给我们的直观感受就是:当实际标签和预测结果相同时,即y和同时为1或0,此时代价最小为0; 当实际标签和预测标签恰好相反时,也就是恰好给出了错误的答案,此时惩罚最大为正无穷。现在应该可以感受到对数损失之于LR的好了。
为了可以更加方便的进行后面的参数估计求解,我们可以把Cost表示在一行:
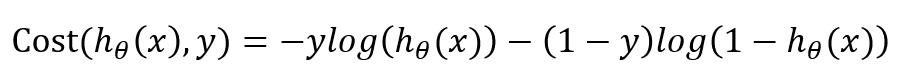
这与我们之前给出的两行表示的形式是等价的。因此,我们的代价函数最终形式为:
该函数是一个凸函数,这也达到了我们的要求。这也是LR代价函数最终形式。
代价函数的求导过程
Sigmoid函数的求导过程:
故,sigmoid函数的导数 $$ g' = g(1-g) $$
损失函数梯度求解过程:
故,参数更新公式为:
对于LR分类模型的评估,常用AUC来评估,关于AUC的更多定义与介绍,可见参考文献2,在此只介绍一种极简单的计算与理解方法。
对于下图的分类:
对于训练集的分类,训练方法1和训练方法2分类正确率都为80%,但明显可以感觉到训练方法1要比训练方法2好。因为训练方法1中,5和6两数据分类错误,但这两个数据位于分类面附近,而训练方法2中,将10和1两个数据分类错误,但这两个数据均离分类面较远。
AUC正是衡量分类正确度的方法,将训练集中的label看两类{0,1}的分类问题,分类目标是将预测结果尽量将两者分开。将每个0和1看成一个pair关系,团中的训练集共有 5*5=25 个 pair 关系,只有将所有pair关系一至时,分类结果才是最好的,而auc为1。在训练方法1中,与10相关的pair关系完全正确,同样9、8、7的pair关系也完全正确,但对于6,其pair关系(6,5)关系错误,而与4、3、2、1的关系正确,故其auc为(25-1)/25=0.96;对于分类方法2,其6、7、8、9的pair关系,均有一个错误,即(6,1)、(7,1)、(8,1)、(9,1),对于数据点10,其正任何数据点的pair关系,都错误,即(10,1)、(10,2)、(10,3)、(10,4)、(10,5),故方法2的auc为(25-4-5)/25=0.64,因而正如直观所见,分类方法1要优于分类方法2。
正则:机器学习中正则化项L1和L2的直观理解 https://blog.csdn.net/jinping_shi/article/details/52433975
此时的w为θ。
对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
此时加入的正则化项,是解决过拟合问题。
下图是Python中Lasso回归的损失函数,式中加号后面一项即为L1正则化项。
下图是Python中Ridge回归的损失函数,式中加号后面一项即为L2正则化项。
一般回归分析中回归w表示特征的系数,从上式可以看到正则化项是对系数做了处理(限制)。L1正则化和L2正则化的说明如下:
一般都会在正则化项之前添加一个系数,Python中用α表示,一些文章也用λ表示。这个系数需要用户指定。
那添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
这部分内容将解释为什么L1正则化可以产生稀疏模型(L1是怎么让系数等于零的),以及为什么L2正则化可以防止过拟合。
稀疏模型与特征选择:
上面提到L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。为什么要生成一个稀疏矩阵?
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
假设有如下带L1正则化的损失函数:
其中J0是原始的损失函数,加号后面的一项是L1正则化项,α是正则化系数。注意到L1正则化是权值的绝对值之和,J是带有绝对值符号的函数,因此J是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当我们在原始损失函数J0后添加L1正则化项时,相当于对J0做了一个约束。令L=,则J=J0+LJ,此时我们的任务变成在L约束下求出J0取最小值的解。考虑二维的情况,即只有两个权值w1和w2,此时L=|w1|+|w2|对于梯度下降法,求解J0的过程可以画出等值线,同时L1正则化的函数L也可以在w1、w2的二维平面上画出来。如下图3.10所示。
图3.10 L1正则化图中等值线是J0的等值线,黑色方形是L函数的图形。在图中,当J0等值线与L图形首次相交的地方就是最优解。上图中0J与L在L的一个顶点处相交,这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)。可以直观想象,因为L函数有很多『突出的角』(二维情况下四个,多维情况下更多),J0与这些角接触的机率会远大于与L其它部位接触的机率,而在这些角上,会有很多权值等于0,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的黑色方框);α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。
类似,假设有如下带L2正则化的损失函数:
同样可以画出他们在二维平面上的图形,如下:
图12 L2正则化
二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此J0与L相交时使得w1或w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』。
那为什么L2正则化可以获得值很小的参数?
以线性回归中的梯度下降法为例。假设要求的参数为θ,hθ(x)是我们的假设函数,那么线性回归的代价函数如下:
那么在梯度下降法中,最终用于迭代计算参数 θ 的迭代式为:
其中α是learning rate. 上式是没有添加L2正则化项的迭代公式,如果在原始代价函数之后添加L2正则化,则迭代公式会变成下面的样子:
其中λ就是正则化参数。从上式可以看到,与未添加L2正则化的迭代公式相比,每一次迭代,θj都要先乘以一个小于1的因子,从而使得θj不断减小,因此总得来看,θ是不断减小的。
L2正则化参数:
从公式5可以看到,λλ越大,θjθj衰减得越快。另一个理解可以参考图2,λλ越大,L2圆的半径越小,最后求得代价函数最值时各参数也会变得很小。
# -*- coding: utf-8 -*-
"""
Created on Sun Jan 5 11:04:11 2019
@author: Yida Zhang
"""
import numpy as np
import pandas as pd
from numpy import dot
from numpy.linalg import inv
iris = pd.read_csv('D:\iris.csv')
dummy = pd.get_dummies(iris['Species']) # 对Species生成哑变量
iris = pd.concat([iris, dummy], axis =1 )
iris = iris.iloc[0:100, :] # 截取前一百行样本
# 构建Logistic Regression , 对Species是否为setosa进行分类 setosa ~ Sepal.Length
# Y = g(BX) = 1/(1+exp(-BX))
def logit(x):
return 1./(1+np.exp(-x))
temp = pd.DataFrame(iris.iloc[:, 0])
temp['x0'] = 1.
X = temp.iloc[:,[1,0]]
Y = iris['setosa'].reshape(len(iris), 1) #整理出X矩阵 和 Y矩阵
# 批量梯度下降法
m,n = X.shape #矩阵大小
alpha = 0.0065 #设定学习速率
theta_g = np.zeros((n,1)) #初始化参数
maxCycles = 3000 #迭代次数
J = pd.Series(np.arange(maxCycles, dtype = float)) #损失函数
for i in range(maxCycles):
h = logit(dot(X, theta_g)) #估计值
J[i] = -(1/100.)*np.sum(Y*np.log(h)+(1-Y)*np.log(1-h)) #计算损失函数值
error = h - Y #误差
grad = dot(X.T, error) #梯度
theta_g -= alpha * grad
print theta_g
print J.plot()
# 牛顿方法
theta_n = np.zeros((n,1)) #初始化参数
maxCycles = 10 #迭代次数
C = pd.Series(np.arange(maxCycles, dtype = float)) #损失函数
for i in range(maxCycles):
h = logit(dot(X, theta_n)) #估计值
C[i] = -(1/100.)*np.sum(Y*np.log(h)+(1-Y)*np.log(1-h)) #计算损失函数值
error = h - Y #误差
grad = dot(X.T, error) #梯度
A = h*(1-h)* np.eye(len(X))
H = np.mat(X.T)* A * np.mat(X) #海瑟矩阵, H = X`AX
theta_n -= inv(H)*grad
print theta_n
print C.plot() [1] 逻辑回归(Logistic Regression) ==偏应用的一篇== 原文链接:https://blog.csdn.net/liulina603/article/details/78676723
[2] Logistic Regression(逻辑回归)详细讲解 原文链接:https://blog.csdn.net/joshly/article/details/50494548
[3] 机器学习算法(一):逻辑回归模型(Logistic Regression, LR) 原文链接:https://blog.csdn.net/weixin_39910711/article/details/81607386
[4] 逻辑回归(logistic regression)原理详解 原文链接:https://blog.csdn.net/guoziqing506/article/details/81328402
[5] 史上最直白的logistic regression教程 之 一 原文链接:https://blog.csdn.net/lizhe_dashuju/article/details/49864569
[6] 机器学习中正则化项L1和L2的直观理解 原文链接:https://blog.csdn.net/jinping_shi/article/details/52433975